PrubehFunkce.mw

Průběh funkce

Předpis funkce:

Pracujeme s reálnými funkcemi:

> with(RealDomain);

Warning, these protected names have been redefined and unprotected: Im, Re, ^, arccos, arccosh, arccot, arccoth, arccsc, arccsch, arcsec, arcsech, arcsin, arcsinh, arctan, arctanh, cos, cosh, cot, coth, csc, csch, eval, exp, expand, limit, ln, log, sec, sech, signum, simplify, sin, sinh, solve, sqrt, surd, tan, tanh

[Im, Re, ^, arccos, arccosh, arccot, arccoth, arccsc, arccsch, arcsec, arcsech, arcsin, arcsinh, arctan, arctanh, cos, cosh, cot, coth, csc, csch, eval, exp, expand, limit, ln, log, sec, sech, signum,...[Im, Re, ^, arccos, arccosh, arccot, arccoth, arccsc, arccsch, arcsec, arcsech, arcsin, arcsinh, arctan, arctanh, cos, cosh, cot, coth, csc, csch, eval, exp, expand, limit, ln, log, sec, sech, signum,...[Im, Re, ^, arccos, arccosh, arccot, arccoth, arccsc, arccsch, arcsec, arcsech, arcsin, arcsinh, arctan, arctanh, cos, cosh, cot, coth, csc, csch, eval, exp, expand, limit, ln, log, sec, sech, signum,...

> f := x^3/(x^4+1);

f := x^3/(x^4+1)

Vlastnosti

Definiční obor

(nutno pro každou funkci zvlášť)

> solve(x^4+1=0,x);

Dále limity v bodech nespojitosti (zde uvádíme jen pro úplnost)

> Limit(f, x=a, left)=limit(f, x=a, left);

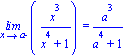
Limit(x^3/(x^4+1), x = a, left) = a^3/(a^4+1)

> Limit(f, x=a, right)=limit(f, x=a, right);

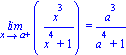
Limit(x^3/(x^4+1), x = a, right) = a^3/(a^4+1)

Je funkce sudá (příp. lichá)?

je několik způsobů, jak ukázat, že je: LICHÁ:  f(x) = –f(–x)

> eval(f,x=-x);
evalb(eval(f,x=x)=-eval(f,x=-x));

-x^3/(x^4+1)

true

> iszero(eval(f,x=x)+eval(f,x=-x));

iszero(0)

> type(f,oddfunc(x));

true

nebo SUDÁ: f(x) = f(–x)

> evalb(eval(f,x=x)=eval(f,x=-x));

false

> type(f,evenfunc(x));

false

První derivace

> df := diff(f,x);

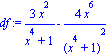
df := 3*x^2/(x^4+1)-4*x^6/(x^4+1)^2

> NuloveBody := solve(df = 0,x);

NuloveBody := 0, 0, 3^(1/4), -3^(1/4)

> Rostoucí := solve(df>0,x);
Klesající := solve(df<0,x);

Rostoucí := RealRange(Open(-3^(1/4)), Open(0)), RealRange(Open(0), Open(3^(1/4)))

Klesající := RealRange(-infinity, Open(-3^(1/4))), RealRange(Open(3^(1/4)), infinity)

Druhá derivace

> d2f := diff(df,x);
d2f := diff(f,x$2);

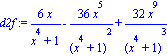
d2f := 6*x/(x^4+1)-36*x^5/(x^4+1)^2+32*x^9/(x^4+1)^3

d2f := 6*x/(x^4+1)-36*x^5/(x^4+1)^2+32*x^9/(x^4+1)^3

Inflexní body

> InflexníBod := solve(d2f = 0,x);

InflexníBod := 0, -(6+33^(1/2))^(1/4), (6+33^(1/2))^(1/4), -(6-33^(1/2))^(1/4), (6-33^(1/2))^(1/4)

> with(Student[Calculus1]):
InflectionPoints(f);

[-(6+33^(1/2))^(1/4), -(6-33^(1/2))^(1/4), 0, (6-33^(1/2))^(1/4), (6+33^(1/2))^(1/4)]

Extrémy

> eval(d2f,x=0);
eval(d2f,x=NuloveBody[3]);
eval(d2f,x=NuloveBody[4]);

0

-3/4*3^(1/4)

3/4*3^(1/4)

Konvexnost a konkávnost

> Konvexní := solve(d2f>0,x);
Konkávní := solve(d2f<0,x);

Konvexní := RealRange(Open(-(6+33^(1/2))^(1/4)), Open(-(6-33^(1/2))^(1/4))), RealRange(Open(0), Open((6-33^(1/2))^(1/4))), RealRange(Open((6+33^(1/2))^(1/4)), infinity)

Konkávní := RealRange(-infinity, Open(-(6+33^(1/2))^(1/4))), RealRange(Open(-(6-33^(1/2))^(1/4)), Open(0)), RealRange(Open((6-33^(1/2))^(1/4)), Open((6+33^(1/2))^(1/4)))

Asymptota se směrnicí

> k:=limit(f/x,x=infinity);

k := 0

> q:=limit(f-x*k,x=infinity);

q := 0

> Asymptota := k*x+q;

Asymptota := 0

A nakonec graf:

> plot([f,Asymptota],x=-10..10);

[Plot]

>